算法调试
假设我们已经实现了一个带有正则化项的线性回归分类器,loss function如下:
图1-1,线性回归loss function
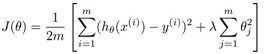
当我们在一个新的测试集上测试模型效果时,有时会发现模型效果比较差,并且超出可接受范围。那下一步该怎么办呢,通常我们会有以下一些常用的方法:
- 增加更多的训练数据
- 减少features
- 增加更多features
- 增加多项式项(比如构造新features x_1^2, x_2^2,或者x_1 * x_2等等)
- 增大正则化项lambda
- 减小正则化项lambda
接下来我们会介绍一些诊断的方法,来帮我们找到哪些方法在现有情况下是有用的,哪些是没用的,以及我们接下来采取什么方法能最有效。
评估分类器
首先我们定义一个简单的标准,来评估我们学习出的分类器好坏。
假设我们现在已经得到一个分类器,在训练数据上的拟合效果如下图。
图1-2,overfitting example
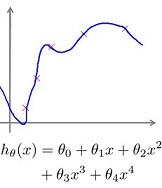
我们可以猜想,这个分类器的泛化性不会太好。虽然在训练集上的效果非常好,但是在预测一些从未在训练集出现的新样本时,效果就会比较差。我们把这种现象叫过拟合,后面会再详细介绍。
training set error最小化并不是我们的最终目标,我们的最终目标是最小的test set error. 实际上我们总是能找到一个分类器使我们的training set error降到0.
所以,当我们拿到一份标注数据,会将数据划分成两份,分别为 training set 和 test set, 划分比例通常分别为70%和30%, 最终在training set上训练,在test set上测试的error作为我们分类器好坏的标准。
对于线性回归,training/testing的过程如下:
- 在training set(70%)上学习 theta, 该 theta 使training error J(theta) 最小;
- 在test set(30%)上计算test set error.
对于线性回归,test set error的计算方式可以为
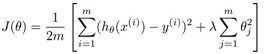
对于逻辑回归,test set error的计算方式可以为
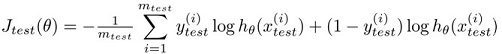
其实就是利用 loss function 作为 test error.
模型选择和训练/验证/测试集
过拟合(Overfitting)
图1-2中是一个overfitting的例子。
在这种情况下,过于拟合训练集,training error通常会明显低于test set error,而这并不是我们想要的结果。
模型选择(Model Selection)
假设我们只有一个feature,通过增加多项式项,构造出如下10个models
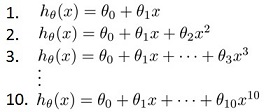
我们可以根据前面的方法,在占总数据30%的测试集上进行测试,选出一个效果最好的model,假设我们选到了第5个,test set error 记为J5.
这样会有带来一个问题:J5相对于model的泛化误差,很有可能是一个偏乐观的估计。因为在我们选择的过程中,会倾向于去拟合测试集,评估结果基于测试集进行了优化,而其中的变量,则是这个选择过程新引入的一个变量,多项式的系数 d (在上面的例子中d为1到10的数).
我们该如何评估模型效果?
为了解决上面的问题,我们引入第三个集合:交叉验证集。我们用交叉验证集选择参数,而只在测试集上评估模型效果。
一种典型的划分方法是训练集占60%,交叉验证集和测试集各占20%.
这样我们可以定义3种误差,分别为
training error
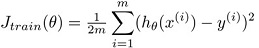
cross validation error
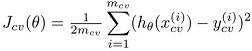
test error
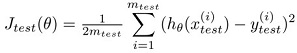
所以,我们最终选择模型的方法,就是利用交叉验证集选择最优的参数,但是用测试集估计模型的泛化误差。
bias/variance分析
对于bias和variance的定义,可以看一下下面这段字,是从大CMU的考试题里摘出来的,讲的比较简单易懂。

在线性回归中,下图非常直观
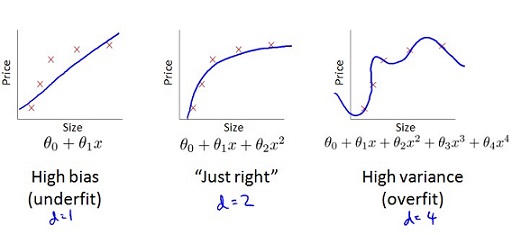
在我们进行模型选择,在验证集上进行参数选择,当多项式系数 d 变化时,training error 和 cross validation error 变化过程如下图。
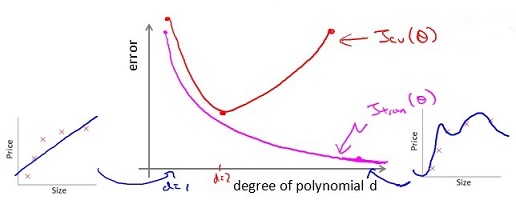
图中红色的线为 cross validation error, 粉色的线为 training error.
d 增加的过程中,目标函数的 bias 减小, variance 增大,从欠拟合到最后过拟合。当cross validation error J_cv 开始增加时(途中红色线的拐点),开始过拟合。
那么,当我们发现 cross validation error J_cv 很大时,该如何判断目前是处于欠拟合还是过拟合呢? 还是先来看看下面的图:
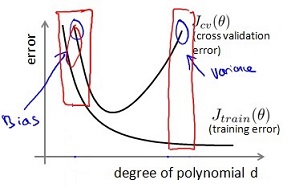
当观察到 J_cv 很大时,可能处在途中蓝色圆圈中的两个位置,虽然观察到的现象很相似(J_cv都很大),但这两个位置的状态是非常不同的,处理方法也完全不同。
当处于图中标出的bias时,此时 high bias low variance,处于欠拟合状态。
当处于图中标出的variance时,此时 low bias high variance,处于过拟合状态。
分别这两种状态的方法和操作建议如下:
- 当 J_train很高,同时 J_cv也很大时,J_train =~ J_cv, 处于欠拟合状态,即此时high bias low variance. 对应上图中 “bias” 那个点,此时应该增大 d;
- 当 J_train很小,同时 J_cv 很大时,J_cv » J_train, 处于过拟合状态,即此时low bias high variance. 对应上图中 “variance” 那个点,此时应该减小 d.
正则化项的影响
正则化项的出现,是为了防止算法在训练过程中过拟合,即防止 high variance。但是过大的正则化,会使训练过程欠拟合,即出现 high bias. 本节我们主要讲如何选择合适的正则化参数 lambda.
正则化项参数 lambda 对模型的影响如下图所示:
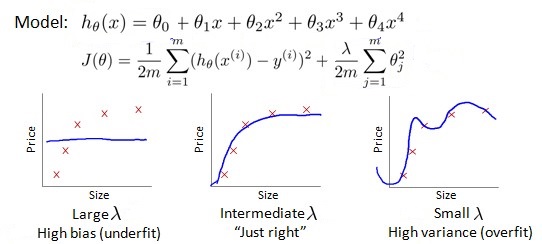
从上面这张图可以很清楚的看到三种状态下 lambda 对于最终模型的影响。
对于lambda的选择,还是与上面提到的方法一致,利用验证集筛选,最终在测试集上的结果作为模型的泛化误差估计。
下面这张图,能更加直观的反映出当 lambda 变化时,对 bias/variance 的影响:
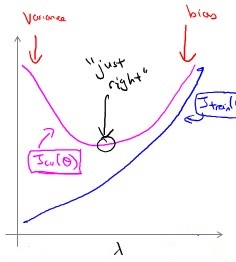
图中粉色的线表示验证集上的error J_cv, 蓝色的线表示训练集上的error J_train.
当 lambda 较小时,更容易过拟合,这也是 lambda 存在的使命 —— 防止过拟合。同样的,当我们观察到 J_cv 很大时,需要调节 lambda,使得模型走到 “just right” 的点。面临到问题是向左走还是向右走。
如何区分是在 “variance” 还是 “bias”, 与之前调节多项式系数 d 遇到的问题一样,所以判断方式也是类似的,从上图可以轻易看出,判断方法和操作建议如下:
- 当 J_train 很低,同时 J_cv 很大时, J_cv » J_train,处于过拟合状态,即此时 low bias high variance. 对应上图中 “variance” 那个点,此时应该增大 lambda;
- 当 J_train 很大,同时 J_cv 也很大时, J_cv =~ J_train,处于欠拟合状态,即此时 high bias low variance. 对应上图中 “bias” 那个点,此时应该减小 lambda.
学习曲线(learning curves)
验证集误差和训练误差随着训练数据增加的变化趋势一般如下图:
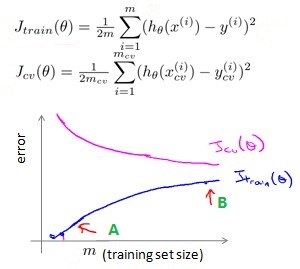
蓝色的线表示训练集上的误差 J_train, 粉色的线表示验证集上的误差 J_cv,横轴表示训练集合的大小。
刚开始处于 “A” 点,表示当训练数据很小时,很容易时训练集上的误差非常小,此时处于过拟合状态。随着训练数据的增加,训练数据上的误差 J_train 越来越大,而验证集上的误差 J_cv 越来越小,J_train 和 J_cv 越来越接近但始终保持 J_cv > J_train.
下面讨论何时增加训练数据能提升模型效果,何时增加训练数据也不会带来更多提升。
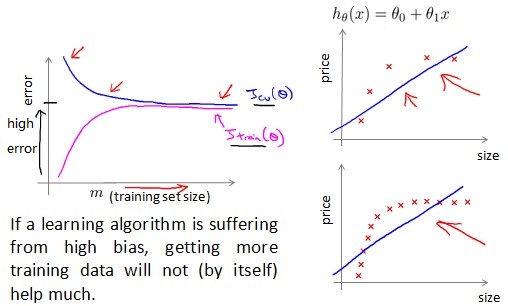
High bias
当模型处于 high bias 的状态时,增加更多的训练数据并不能提升效果。此时我们的目标函数拟合能力太差。典型的例子如下图,比如我们的训练数据分布为二次曲线,但如果用线性函数去拟合,增加数据并不能降低 error.
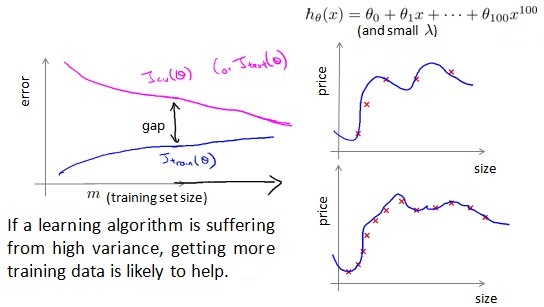
High variance
当模型处于 high variance 的状态时,增加更多的训练数据能明显提升效果。此时我们的目标函数拟合能力非常好,但是当数据很少时,很容易发生过拟合。这个时候我们补充更多的数据,会带来更多的信息含量,数据量多也更不容易发生过拟合。
回顾
再来回顾一下刚开始的问题。
假设我们已经实现了一个带有正则化项的线性回归分类器,当我们在一个新的测试集上测试时发现效果比较差时,我们通常采用的方法和这些方法真正的作用:
- 增加更多的训练数据 —— 修复 high variance 的问题
- 减少features —— 修复 high variance 的问题
- 增加更多features —— 修复 high bias 的问题
- 增加多项式项 —— 修复 high bias 的问题
- 增大正则化项lambda —— 修复 high variance 的问题
- 减小正则化项lambda —— 修复 high bias 的问题
我们前面介绍的一些方法,可以从我们观察到的现象判断处在什么状态,从而采取合适的方法提升模型的效果。